Mensuration Formula in Hindi – आज के इस पोस्ट में हम आपको कंपटीशन Exams के सबसे महत्वपूर्ण टॉपिक mensuration formula in hindi (क्षेत्रमिति के सभी फार्मूला ) या mensuration formula in hindi pdf के साथ देने वाले हैं जिसके द्वारा आप अपने प्रतियोगी परीक्षाओं में अच्छा अंक प्राप्त कर सकते हैं|
Visit Our Website – upboardnotes.in
Mensuration Formula पढ़ने से पहले सबसे पहले आपको क्षेत्रफल ,परिमाप तथा आयतन की जानकारी होना आवश्यक है जिसका नीचे आपको संक्षिप्त में उल्लेख किया गया है |
Mensuration Formula in Hindi
क्षेत्रफल—किसी आकृति की भुजाओं से घिरे हुए क्षेत्र या तल की उस आकृति का क्षेत्रफल कहते हैं।
परिमाप—किसी आकृति की भुजाओं की लम्बाइयों का योग या आकृति की सीमा की लवाई को उस आकृति का परिमाप (परिमिति) कहते हैं।
आयतन– कोई वस्तु जितना स्थान घेरती है, उसे उस वस्तु का आयतन कहते है।
Mensuration All Formula in Hindi | क्षेत्रमिति के सभी फार्मूला
1.त्रिभुज (Triangle)
तीन रेखाखंडों से घिरी हुई बंद आकृति को त्रिभुज कहते हैं।त्रिभुज में तीन कोण LA, LB, LC तथा त्रिभुज की तीन भुजाएँ AB, BC तथा CA है।
(i) त्रिभुज का परिमाप = AB + BC + CA = तीनों भुजाओं का योग
(ii) त्रिभुज का क्षेत्रफल =1/2x आधार x ऊँचाई (संगत शीर्षलम्ब)
(iii) समकोण त्रिभुज– जिस त्रिभुज का एक को समकोण (90°) हो, उस त्रिभुज को समकोण
त्रिभुज कहते हैं।
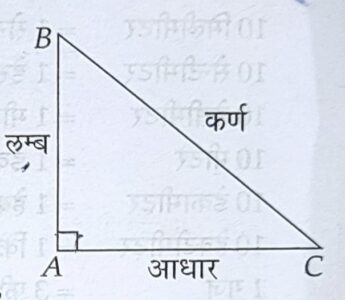
समकोण त्रिभुज में सबसे बड़ी भुजा (समकोण शीर्ष के सम्मुख भुजा) कर्ण कहलाती है।
समकोण त्रिभुज में सबसे बड़ी भुजा का वर्ग अन्य दो भुजाओं के वर्गों के योग के बराबर होता है।

(iv) समकोण त्रिभुज का क्षेत्रफल = 1/2लम्बx आधार
=1/2x समकोण बनाने वाली भुजाओं का गुणनफल
(v) समकोण त्रिभुज का परिमाप = तीनों भुजाओं का योग
2. आयत (Rectangle)
आयत – वह चतुर्भुज है, जिसकी आमने सामने की भुजायें बराबर तथा प्रत्येक कोण समकोण हों, आयत कहलाते हैं।
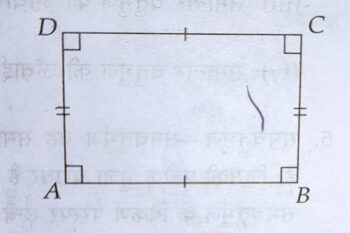
(i) आयत का परिमाप = 2(लम्बाई + चौड़ाई)
(ii) आयत का क्षेत्रफल = लंबाई ×चौड़ाई
(iii) आयत का विकर्ण =√(लंबाई² + चौड़ाई²)
3. वर्ग (Square)
वर्ग – एक वैसा चतुर्भुज है, जिसकी सभी भुजायें बराबर तथा प्रत्येक कोण 90° का होता है।
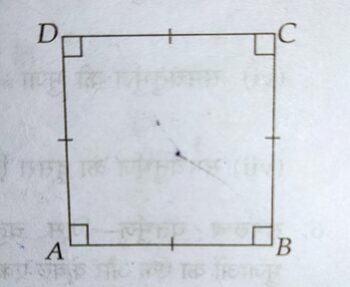
(i) वर्ग का क्षेत्रफल = भुजा² = भुजा x भुजा
(ii) वर्ग की भुजा = √ वर्ग का क्षेत्रफल
(iii) वर्ग का परिमाप = 4 x भुजा
(iv) वर्ग की भुजा = परिमाप/4
(v) वर्ग का विकर्ण =√ 2x भुजा
(vi) वर्ग की भुजा = विकर्ण/√2
4.समान्तर चतुर्भुज या समानान्तर चतुर्भुज ( Parallelogram )
समानान्तर चतुर्भुज – वैसा चतुर्भुज जिसके आमने- सामने की भुजायें समान तथा समांतर हों, समांतर चतुर्भुज कहलाता है।
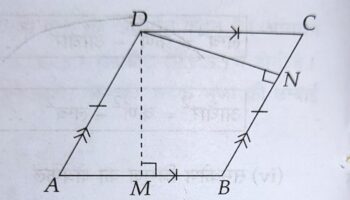
(i) समान्तर चतुर्भुज का क्षेत्रफल = आधार x ऊँचाई (संगत शीर्षलम्ब)
समान्तर चतुर्भुज ABCD का क्षेत्रफल = ABx DM या, BC × DN
(ii) समान्तर चतुर्भुज का परिमाप = 2 x (आसन्न भुजाओं का एक युग्म का योग)
(iii) समान्तर चतुर्भुज का आधार (एक भुजा) = क्षेत्रफल /ऊँचाई(संगतःशीर्षलम्ब )
(iv) समान्तर चतुर्भुज की ऊँचाई = क्षेत्रफल/आधार
5.समचतुर्भुज (Rhombus)
समचतुर्भुज – वह समान्तर चतुर्भुज है, जिसकी प्रत्येक भुजा बराबर है। समचतुर्भुज के विकर्ण परस्पर लम्ब समद्विभाग करते हैं।
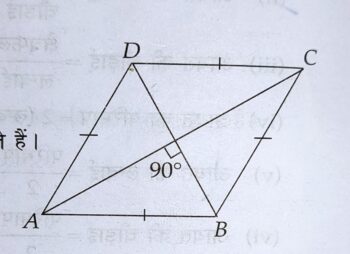
(i) समचतुर्भुज का क्षेत्रफल = आधार x ऊँचाई
(ii) समचतुर्भुज की आधार (भुजा) = समचतुर्भुज का क्षेत्रफल/ऊँचाई
(iii) समचतुर्भुज की ऊँचाई = समचतुर्भुज का क्षेत्रफल/आधार
(iv) समचतुर्भुज की परिमिति = 4 x एक भुजा की लम्बाई
(v) समचतुर्भुज का क्षेत्रफल = 1/2 × विकर्णों का गुणनफल
6. समलंब चतुर्भुज (Trapezium)
समलम्ब चतर्भुज – जिस चतुर्भुज के सम्मुख भुजाओं का एक और केवल एक युग्म समान्तर हो, उस चतुर्भुज को समलम्ब चतुर्भुज कहते हैं।

(i) समलम्ब चतुर्भुज का क्षेत्रफल = 1/2 × (समान्तर भुजाओं का जोड़) x ऊँचाई
(ii) समलम्ब चतुर्भुज की ऊँचाई (समान्तर भुजाओं के बीच की दूरी) = 2×समलम्ब चतुर्भुज का क्षेत्रफल/समान्तर भुजाओं का जोड़ (योग)
7. वृत्त ( Circle )
वृत्त — वह आकृति जो एक गतिमान बिन्दु-पथ के चारों ओर एक निश्चित दूरी पर चलता है, वृत्त कहलाती है। स्थिर बिन्दु को वृत्त का केन्द्र कहते हैं।
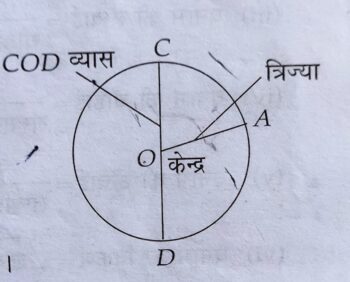
त्रिज्या-वृत्त के केन्द्र से वृत्त के किन्हीं बिन्दु को मिलाने वाली रेखाखंड वृत्त की त्रिज्या कहलाती है ।
एक वृत्त में अनंत त्रिज्यायें खींची जा सकती हैं।
वृत्त का व्यास–वृत्त की परिधि के किन्हीं दो बिन्दुओं को मिलाने वाली रेखाखंड जो केन्द्र से होकर गुजरती हो, व्यास कहलाती है।
एक वृत्त में अनन्त व्यास खींचे जा सकते हैं।
(i) वृत्त का क्षेत्रफल = πr²
(ii) वृत्त का व्यास = 2r
(iii) वृत्त की परिधि = 2πr
(iv) वृत्त की परिधि = πd
(v) वृत्त की त्रिज्या = √व्रत का क्षेत्रफल/π
(vi) वृताकार वलय का क्षेत्रफल = π (R2 – r2)
(vii)अर्द्धवृत्त की परिधि = ( π r + 2 r )
(viii) अर्द्धवृत्त का क्षेत्रफल = 1/2πr²
8. घनाभ (Cuboid)
घनाभ– छः आयताकार सतहों से घिरी आकृति घनाभ कहलाती है। घनाभ में छः सतह (पृष्ठ), 8 शीर्ष एवं 12 किनारे होते हैं ।
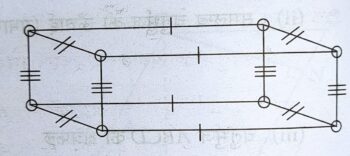
संकेत: O शीर्ष
‘।’ लम्बाई, ॥’, चौड़ाई, ‘|||’ ऊँचाई
(i) घनाभ के सम्पूर्ण पृष्ठों का क्षेत्रफल = 2 (लम्बाई x चौड़ाई + चौड़ाई x ऊँचाई + ऊँचाई ×लम्बाई )
(ii) घनाभ का आयतन = लम्बाई x चौड़ाई x ऊँचाई (गहराई)
(iii) घनाभ की लम्बाई = आयतन/चौड़ाई x ऊँचाई
(iv) घनाभ की चौड़ाई = आयतन/लम्बाई x ऊँचाई
(v) घनाभ की ऊँचाई = आयतन/लम्बाई x चौड़ाई = आयतन/आधार का क्षेत्रफल
(vi) घनाभ का विकर्ण = √( लंबाई² + चौड़ाई² + ऊँचाई²)
(vii) घनाभ के वक्रतल का क्षेत्रफल = 2 (लम्बाई + चौड़ाई) x ऊँचाई
9. घन (Cube)
घन- छः वर्गाकार सतहों से घिरी आकृति घन कहलाती है, जैसे-लुडो का पासा, सुगर क्यूब ।

घन की लम्बाई = घन की चौड़ाई = घन की ऊँचाई
(i) घन के सम्पूर्ण पृष्ठों का क्षेत्रफल = 6 x भुजा²
(ii) धन की भुजा =√सम्पूर्ण पृष्ठों का क्षेत्रफल/6
(iii) धन का आयतन = भुजा³
(iv) घन की भुजा = ³√आयतन
(v) घन का विकर्ण = √3x भुजा
(vi) धन की भुजा – विकर्ण/√3
(vii) धन के वक्र पृष्ठ का क्षेत्रफल = 4 x भुजा²
(viii) कमरे के चारों दीवारों का क्षेत्रफल = 2(लम्बाई + चौड़ाई) x ऊँचाई अथवा परिमिति x ऊँचाई
(ix) कमरे की ऊँचाई = कमरे के चारों दीवारों का क्षेत्रफल /कमरे की परिमिति





